四次素数

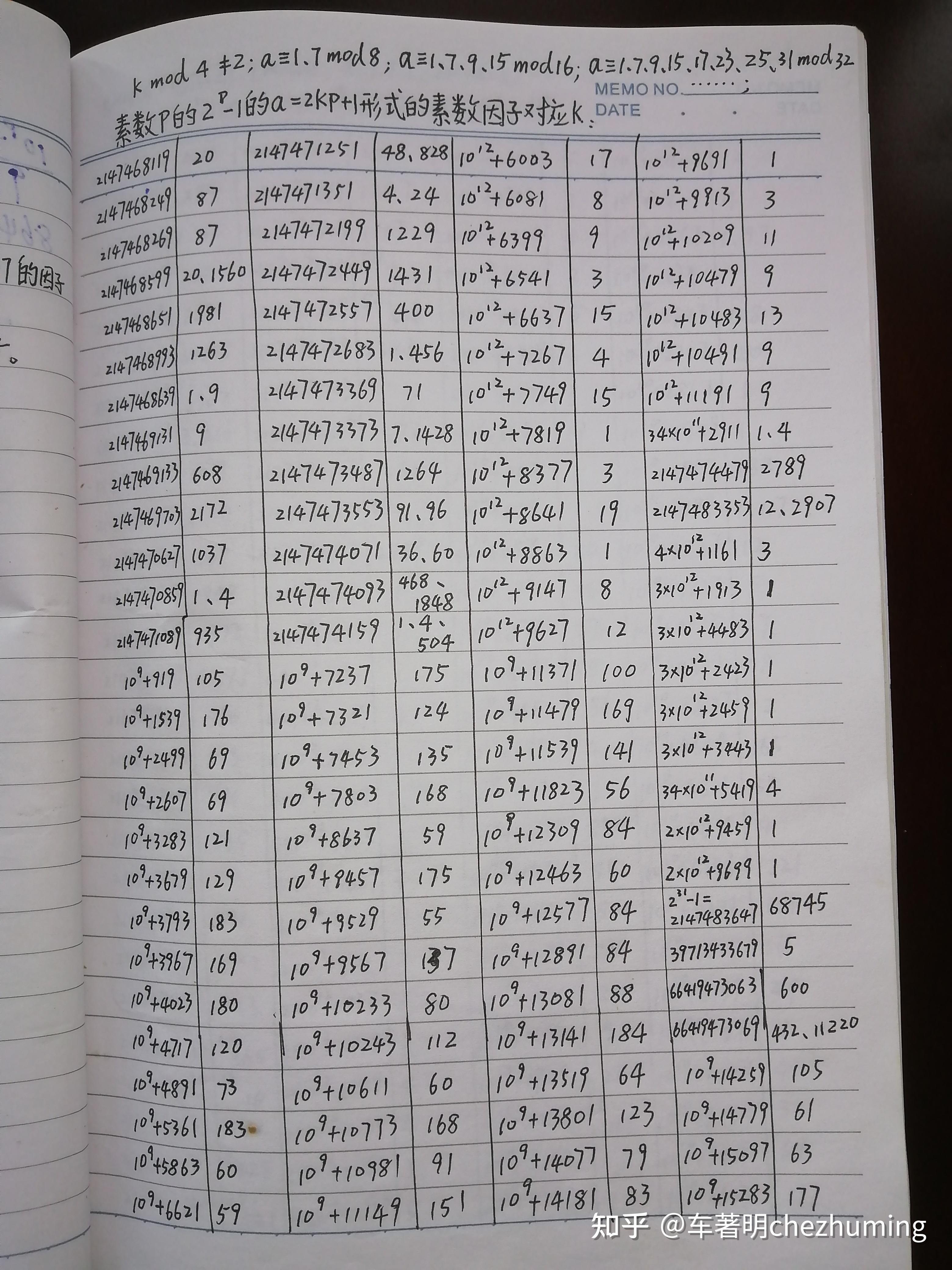
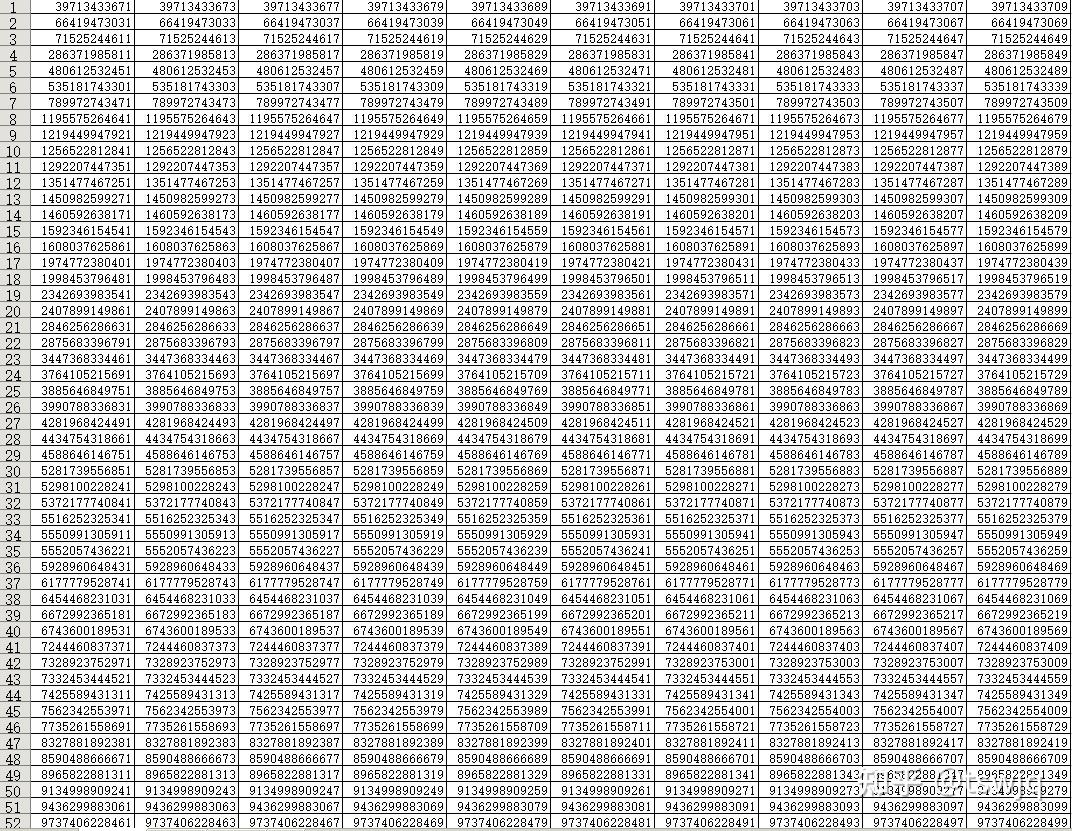
数学における、四次素数（よじそすう、英:Quartan prime）とは正のx,yを用いて${\displaystyle x^{4} y^{4}}$と表される素数のことである。奇数の四次素数は${\displaystyle 16n 1}$(nは自然数)の形を取る。

例えば、最小の奇数の四次素数である17は

${\displaystyle 1^{4} 2^{4}=1 16=17}$

と表される。

2の場合(${\displaystyle x=y=1}$)を除いて、xとyはどちらかが奇数、どちらかが偶数になる。両方が奇数または両方が偶数の場合、結果偶数となり唯一の偶数素数である2が当てはまる。

四次素数は小さい順に、

2, 17, 97, 257, 337, 641, 881, … (オンライン整数列大辞典の数列 A002645)

である。

関連項目

• 四乗数
• 四次式

参考文献

• Neil Sloane, A Handbook of Integer Sequences, Academic Press, NY, 1973.